こんにちは。今回は「ラプラス変換って結局何してんの?」という方に向けて原理をわかりやすく解説していきたいと思います。
ラプラス変換を初めて習う方にも分かりやすい図を作ってみたので一緒に頑張りましょう。
ラプラス変換って何?
ちょっとお堅めの定義とか(苦手な方は注意)
$$F(s)=\int_{0}^{\infty}f(t)e^{-st}dt$$
区間\([0,\infty)\)で定義された関数\(f(t)\)が
・区分的に連続
・\(|f(t)|\le Me^{\gamma t}\) \((M\gt0,\gamma\gt0)\)を満たす\(M\)と\(\gamma\)がある
とき\(s\gt\gamma\)の全ての\(s\)についてラプラス変換\(F(s)\)が存在する。
ラプラス変換を使うメリット
ラプラス変換の何がありがたいかというと、微分方程式の初期値問題を代数計算で扱えるようになるということです。
簡単に言うと、
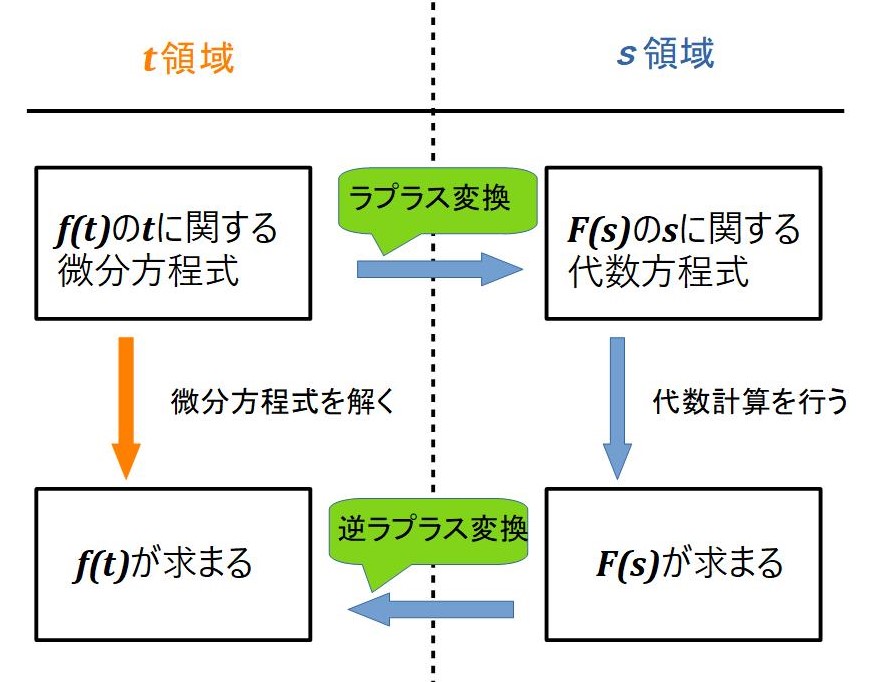
ちなみに代数方程式というのはあなたもよく知る
$$y-2x+4=0$$
のような普通の方程式であり、微分方程式と区別するための記述です。
ラプラス変換表
ラプラス変換は広義積分により定義されています。
しかし、微分方程式を解く場合は以下のラプラス変換表を用いて解くことが一般的です。(後述の例題で見ていただければわかりやすいと思います)
表1.基本的な関数のラプラス変換
| 番号 | $$f(t)$$ | $$F(s)$$ | |
| $$N1$$ | $$1$$ | $$\frac{1}{s}$$ | |
| $$N2$$ | $$t$$ | $$\frac{1}{s^{2}}$$ | |
| $$N3$$ | $$t^{n}$$ | $$\frac{n!}{s^{n+1}}$$ | |
| $$N4$$ | $$e^{-at}$$ | $$\frac{1}{s+a}$$ | |
| $$N5$$ | $$te^{-at}$$ | $$\frac{1}{(s+a)^{2}}$$ | |
| $$N6$$ | $$\mathrm{sin}\omega t$$ | $$\frac{\omega}{s^{2}+\omega^{2}}$$ | 詳細 |
| $$N7$$ | $$\mathrm{cos}\omega t$$ | $$\frac{s}{s^{2}+\omega^{2}}$$ | 詳細 |
| $$N8$$ | $$\mathrm{sinh}\alpha t$$ | $$\frac{s}{s^{2}-\alpha^{2}}$$ | |
| $$N9$$ | $$\mathrm{cosh}\alpha t$$ | $$\frac{\alpha}{s^{2}-\alpha^{2}}$$ | |
| $$N10$$ | $$t\mathrm{sin}\omega t$$ | $$\frac{2\omega s}{(s^{2}+\omega^{2})^{2}}$$ | |
| $$N11$$ | $$t\mathrm{cos}\omega t$$ | $$\frac{s^{2}-\omega ^{2}}{(s^{2}+\omega^{2})^{2}}$$ | |
| $$N12$$ | $$e^{-at}\mathrm{sin}\omega t$$ | $$\frac{\omega}{(s+a)^{2}+\omega^{2}}$$ | |
| $$N13$$ | $$e^{-at}\mathrm{cos}\omega t$$ | $$\frac{s+a}{(s+a)^{2}+\omega^{2}}$$ | |
| $$N14$$ | $$te^{-at}\mathrm{sin}\omega t$$ | $$\frac{2\omega(s+a)}{\{(s+a)^{2}+\omega^{2}\}^{2}}$$ | |
| $$N15$$ | $$te^{-at}\mathrm{cos}\omega t$$ | $$\frac{(s+a)-\omega^{2}}{\{(s+a)^{2}+\omega^{2}\}^{2}}$$ |
表2.ラプラス変換の基本公式
| 番号 | 名称 | $$f(t)$$ | $$F(s)$$ |
| $$n1$$ | 線形定理1 | $$af(t)$$ | $$aF(s)$$ |
| $$n2$$ | 線形定理2 | $$a_1f_1(t)+a_2f_2(t)$$ | $$a_1F_1(s)+a_2F_2(s)$$ |
| $$n3$$ | 相似定理 | $$f(at)$$ | $$\frac{1}{a}F(\frac{s}{a})$$ |
| $$n4$$ | 時間推移定理 | $$f(t-a)u(t-a)$$ | $$e^{-as}F(s)$$ |
| $$n5$$ | 複素推移定理 | $$e^{-at}f(t)$$ | $$F(s+a)$$ |
| $$n6$$ | 微分定理 | $$\frac{df(t)}{dt}$$ | $$sF(s)-f(0)$$ |
| $$n7$$ | 積分定理 | $$\int f(t)dt$$ | $$\frac{F(s)}{s}+\frac{f^{(-1)}(0)}{s}$$ |
※\(u(t)\)は単位インパルス関数
ラプラス変換を行う際は\(f(t)\)→\(F(s)\)、逆ラプラス変換する際は\(F(s)\)→\(f(t)\)の向きで表を見ます。
微分方程式をラプラス変換で解く手順
②\(F(S)\)について式を整理する。
③\(F(S)\)を部分分数に展開。(逆ラプラス変換できる形にするため)
④逆ラプラス変換を用いて\(f(t)\)を求める。
もう一度先ほどの図を見てみましょう。

なんとなくイメージがつかめましたか?
それでは、例題でさらに詳しく見てみましょう。
微分方程式\(\frac{df(t)}{dt}+5f(t)+5=0\)を解け。
ただし、初期条件\(f(0)=0\)、\(t>0\)とする。
ラプラス変換による解法
①微分方程式にラプラス変換を施す。
$$\frac{df(t)}{dt}=-5f(t)-5$$
$$↓ラプラス変換$$
$$sF(s)-f(0)=-5F(s)-\frac{5}{s}$$
初期条件\(f(0)=0\)より
$$sF(s)=-5F(s)-\frac{5}{s}$$
②\(F(s)\)について式を整理する。
$$sF(s)+5F(s)=-\frac{5}{s}$$
$$F(s)(s+5)=-\frac{5}{s}$$
$$F(s)=-\frac{5}{s(s+5)}$$
③\(F(s)\)を部分分数に展開。
$$F(s)=-\frac{5}{s(s+5)}$$
上式右辺を
$$\frac{A}{s}+\frac{B}{s+5}$$
に部分分数分解する。
$$\frac{A}{s}+\frac{B}{s+5}=\frac{A(s+5)+Bs}{s(s+5)}=-\frac{5}{s(s+5)}$$
係数比較をすることにより、以下の2式を得る。
\(A+B=0\)
\(5A=-5\)
\(\therefore\) \(A=-1\),\(B=1\)
$$F(s)=\frac{1}{s+5}-\frac{1}{s}$$
④逆ラプラス変換を用いて\(f(t)\)を求める。
$$F(s)=\frac{1}{s+5}-\frac{1}{s}$$
$$↓逆ラプラス変換$$
$$f(t)=e^{-5t}-1$$
一応直接求める解法も
$$\frac{df(t)}{dt}=-5f(t)-5=-5(f(t)+1)$$
変数分離形に変形すると
$$\frac{1}{f(t)+1}df=-5dt$$
両辺を積分すると
$$log|f(t)+1|=-5t+C$$
$$f(t)+1=\pm e^{-5t+C}=\pm e^{c}e^{-5t}$$
\(\pm e^{C1}\)を新たに\(A\)とおくと(\(C1\),\(A\)は任意定数)
$$f(t)+1=Ae^{-5t}$$
$$f(t)=Ae^{-5t}-1$$
初期条件\(f(0)=0\)より、\(A=1\)
$$\therefore f(t)=e^{-5t}-1$$
まとめ
お疲れさまでした。最後までお付き合いいただきありがとうございます。
定義式は一見難しそうですが、実際の計算では四則演算と式変形の計算がメインです。
例題で慣れてぜひマスターしてみてくださいね!


コメント