RC直列回路の過渡現象を分かりやすく解説！

Tweet

Pocket

お願い）一部数式が長く、モバイル版ではみ出している部分があります。指で画面を縮小していただくと見えるようになります。お手数をおかけしますが、よろしくお願いします。

微分方程式を用いて解く方法

解法

キルヒホッフの第二法則より、回路方程式は

$$E=R\cdot i(t)+\frac{q(t)}{C}$$

また、\(i(t)=\frac{dq(t)}{dt}\) より

$$E=R\cdot \frac{dq(t)}{dt}+\frac{q(t)}{C}$$

\(\frac{dq(t)}{dt}\)について式を整理すると

$$\frac{dq(t)}{dt}=\frac{E}{R}-\frac{q(t)}{RC}=\frac{-1}{RC}(q(t)-CE)$$

変数分離形に変形すると

$$\frac{1}{q(t)-CE}dq(t)=\frac{-1}{RC}dt$$

両辺を\(t\)で積分すると

$$\int\frac{1}{q(t)-CE}dq(t)=\int\frac{-1}{RC}dt$$

$$log|q(t)-CE|=\frac{-1}{RC}t+C1$$

$$q(t)-CE=\pm e^{\frac{-1}{RC}t+C1}=\pm e^{C1}\cdot e^{\frac{-1}{RC}t}$$

\(\pm e^{C1}\)を新たに\(A\)とおくと(\(C1\),\(A\)は任意定数)

$$q(t)=Ae^{\frac{-1}{RC}t}+CE$$

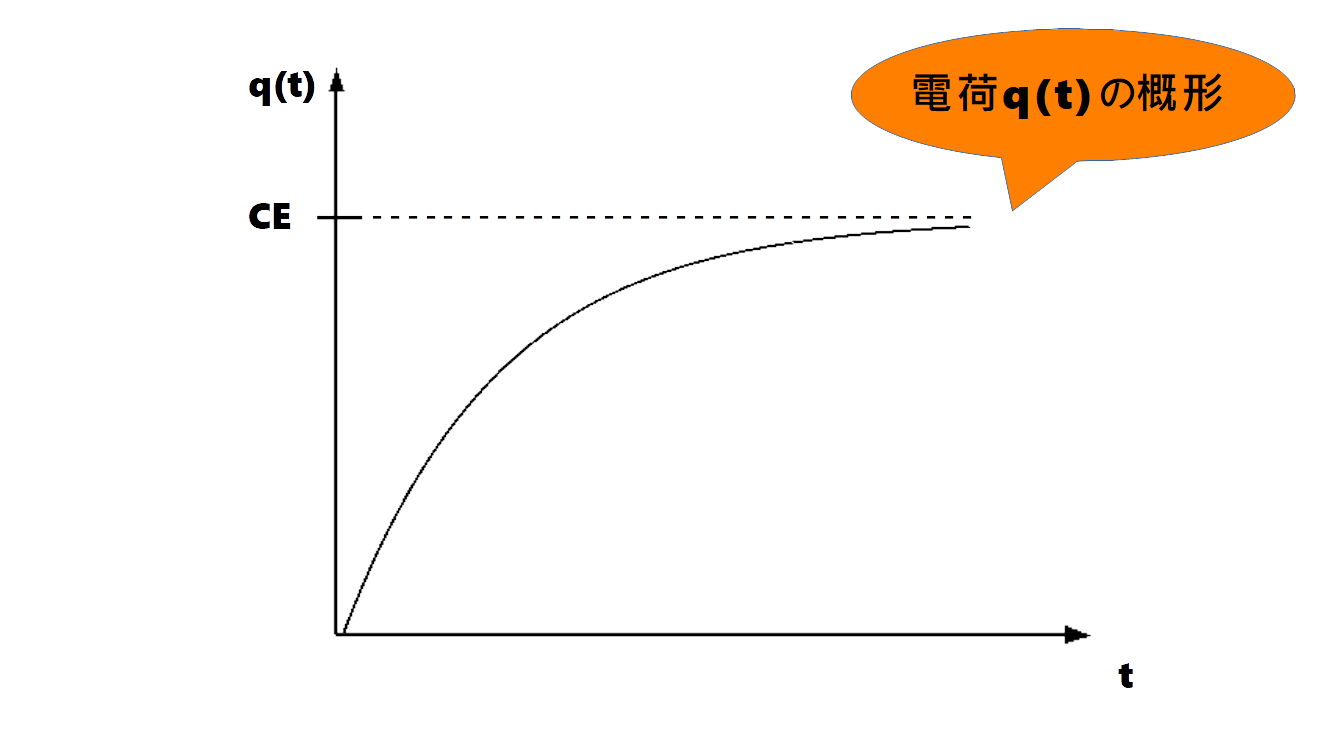
グラフの概形

グラフの概形は下図のようになります。

ラプラス変換を用いて解く方法

キルヒホッフの第二法則より、回路方程式は

$$E=R\cdot i(t)+\frac{q(t)}{C}$$

また、\(i(t)=\frac{dq(t)}{dt}\) より

$$E=R\cdot \frac{dq(t)}{dt}+\frac{q(t)}{C}$$

上式にラプラス変換を施すと

$$\frac{E}{S}=RS\cdot Q(S)-R\cdot q(0)+\frac{Q(S)}{C}$$

初期条件より、\(q(0)=0\)なので

$$\frac{E}{S}=RS\cdot Q(S)-\frac{Q(S)}{C}=Q(S)(RS+\frac{1}{C})$$

これを、\(Q(S)\)について解くと

$$Q(S)=\frac{E}{S^{2}R+\frac{C}{S}}=\frac{E}{R}(\frac{1}{S(S+\frac{1}{RC})})$$

$$Q(S)=\frac{E}{R}(\frac{RC}{S}-\frac{RC}{S+\frac{1}{RC}})$$

$$=CE(\frac{1}{S}-\frac{1}{S+\frac{1}{RC}})$$

上式を逆ラプラス変換すると

次に電流\(i(t)\)を求める。
\(i(t)=\frac{dq(t)}{dt}\)より

まとめ

微分程式とラプラス変換を用いる解法を扱いましたが、どちらも同じ答えになりましたね。

特に指定がなければ、得意な解き方で解けばよいと思います。

ちなみに、\(e^{\frac{-1}{RC}t}\)の\(RC=\tau\)を時定数と呼びますので覚えておきましょう。