RL直列回路の過渡現象を分かりやすく解説！

こんにちは、前回に続いて今回はRL直列回路の過渡現象を扱っていきます。

微分方程式とラプラス変換による解法を紹介するので、やりやすい方で解いてみてください！

問題　以下のRL直列回路において、$t=0$においてスイッチSを閉じる。$t\ge0に$おける電流 $i(t)$を求めなさい。
ただし、$t=0$で電流は流れてないとする。

お願い）一部数式が長く、モバイル版ではみ出している部分があります。指で画面を縮小していただくと見えるようになります。お手数をおかけしますが、よろしくお願いします。

微分方程式を用いて解く方法

キルヒホッフの第二法則より、回路方程式は

$$E=R\cdot i(t)+L\frac{di(t)}{dt}$$

これを、$\frac{di(t)}{dt}$に整理すると

$$\frac{di(t)}{dt}=\frac{E}{L}-\frac{R}{L}\cdot i(t)=-\frac{R}{L}(i(t)-\frac{E}{R})$$

変数分離形に変形すると

$$(\frac{1}{i(t)-\frac{E}{R}})di(t)=-\frac{R}{L}dt$$

両辺を$t$で積分すると

$$\int\frac{1}{i(t)-\frac{E}{R}}di(t)=\int-\frac{R}{L}dt$$

$$log|i(t)-\frac{E}{R}|=-\frac{R}{L}t+C1$$

$$i(t)-\frac{E}{R}=\pm e^{-\frac{R}{L}t+C1}=\pm e^{C1}\cdot e^{-\frac{R}{L}t}$$

$\pm e^{C1}$を新たに$A$とおくと($C1$,$A$は任意定数)

$$i(t)=Ae^{-\frac{R}{L}t}+\frac{E}{R}$$

初期条件より、$i(0)=0$なので
$i(0)=Ae^{0}+\frac{E}{R}=0$
$\therefore A=-\frac{E}{R}$

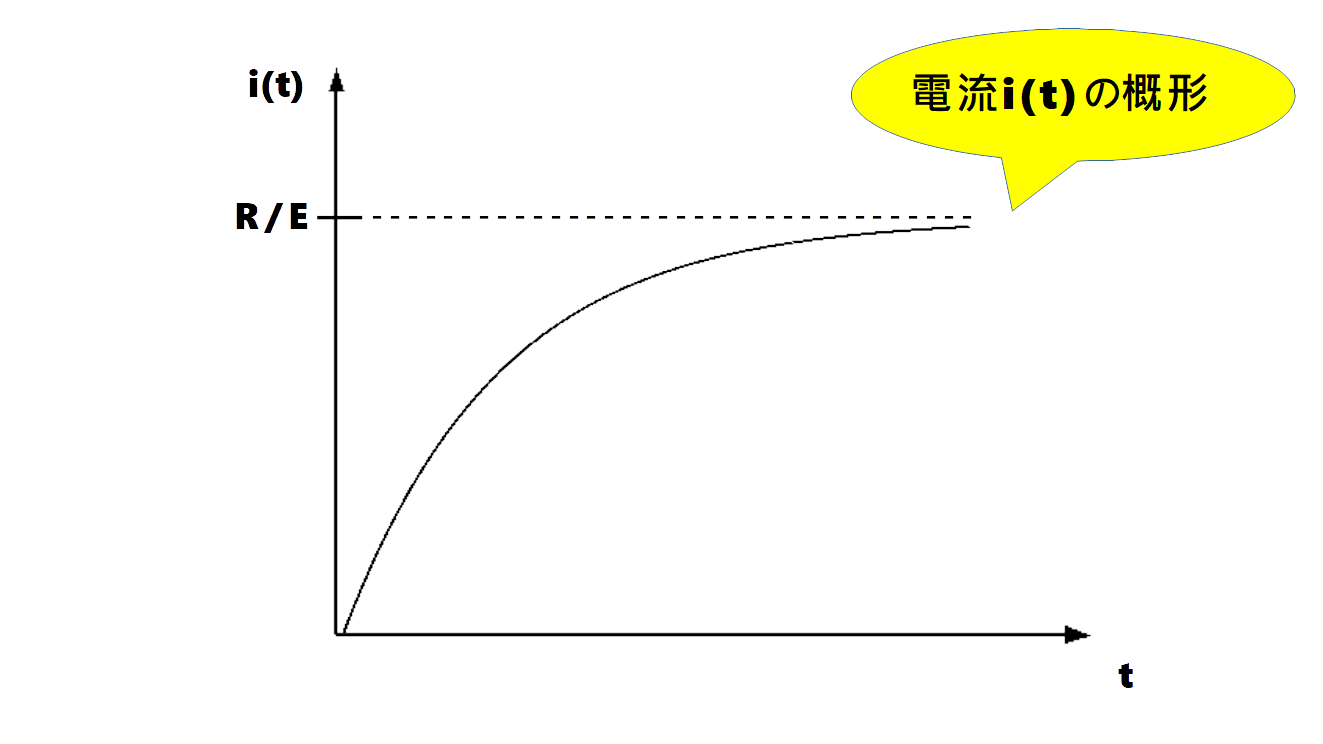
$$i(t)=\frac{E}{R}e^{-\frac{R}{L}t}+\frac{E}{R}=\frac{E}{R}(1-e^{-\frac{R}{L}t})$$

時定数$\tau=\frac{L}{R}$

グラフの概形は下図のようになります。

キルヒホッフの第二法則より、回路方程式は

$$E=R\cdot i(t)+L\frac{di(t)}{dt}$$

上式にラプラス変換を施すと

$$\frac{E}{S}=R\cdot I(S)+S\cdot L\cdot I(S)-i(0)$$

初期条件より、$i(0)=0$なので

$$\frac{E}{S}=R\cdot I(S)+S\cdot L\cdot I(S)$$

これを、$I(S)$について解くと

$$I(S)=\frac{E}{S(SL+R)}=\frac{E}{L}(\frac{1}{S(S+\frac{R}{L})})$$

ラプラス逆変換を行うために部分分数分解を行う。

$$\frac{A}{S}+\frac{B}{S+\frac{R}{L}}=\frac{A(S+\frac{R}{L})+BS}{S(S+\frac{R}{L})}=\frac{1}{S(S+\frac{R}{L})}$$

係数比較により以下の2式を得る
$A+B=1,A\cdot\frac{R}{L}=1$

$\therefore A=\frac{L}{R},B=-\frac{L}{R}$

$$I(S)=\frac{E}{L}(\frac{\frac{L}{R}}{S}-\frac{\frac{L}{R}}{S+\frac{R}{L}})=\frac{E}{R}(\frac{1}{S}-\frac{1}{S+\frac{R}{L}})$$

上式を逆ラプラス変換すると

$$i(t)=\frac{E}{R}(1-e^{-\frac{R}{L}t})$$

時定数$\tau=\frac{L}{R}$

お疲れさまでした。

回路方程式を立てる→ラプラス変換を行う→解きたい変数について整理する→部分分数分解→逆ラプラス変換を行う

とパターンに慣れてしまえばラプラス変換は怖くありません。

たくさん練習して慣れていくと良いと思います。